Алгоритм слияния черновиков

Общий принцип работы

В дереве Entity Groups изменения определяются относительно той ревизии из которой был создан черновик. Изменениями считаются: переименование, перемещение, создание Entity Groups (удаление тоже считается изменением, но не участвует в алгоритме слияния). Затем из изменений образуются поддеревья изменений.

Рассмотрим кейс:

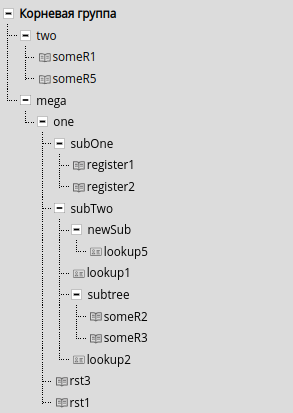
Пользователь переместил subTwo и его реестры lookup1 и lookup2 внутрь группы one. Затем внутрь subTwo переместили группу subTree и ее потомка someR2 и внутри создали новый реестр someR3.

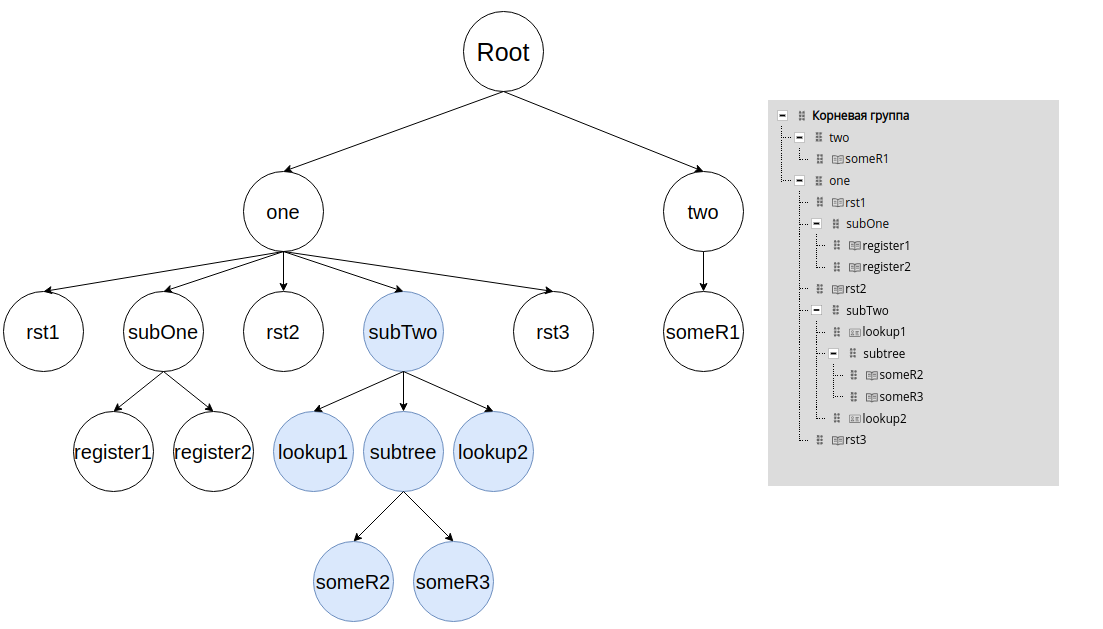
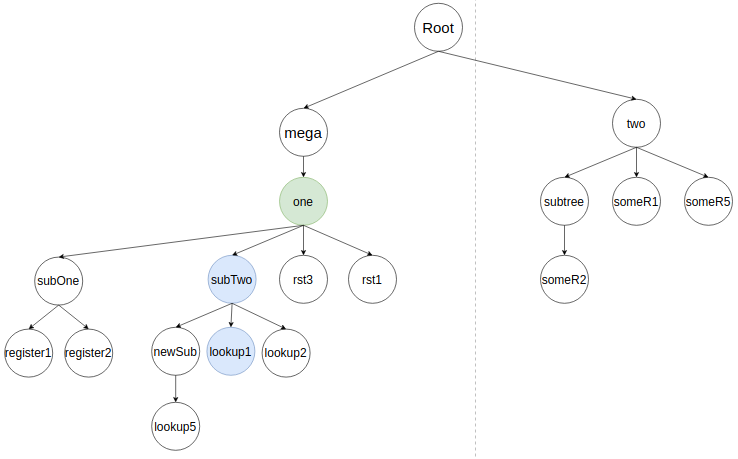
Пока пользователь работал со своей версией модели данных, актуальная версия обновилась и дерево модели данных теперь выглядит следующим образом:

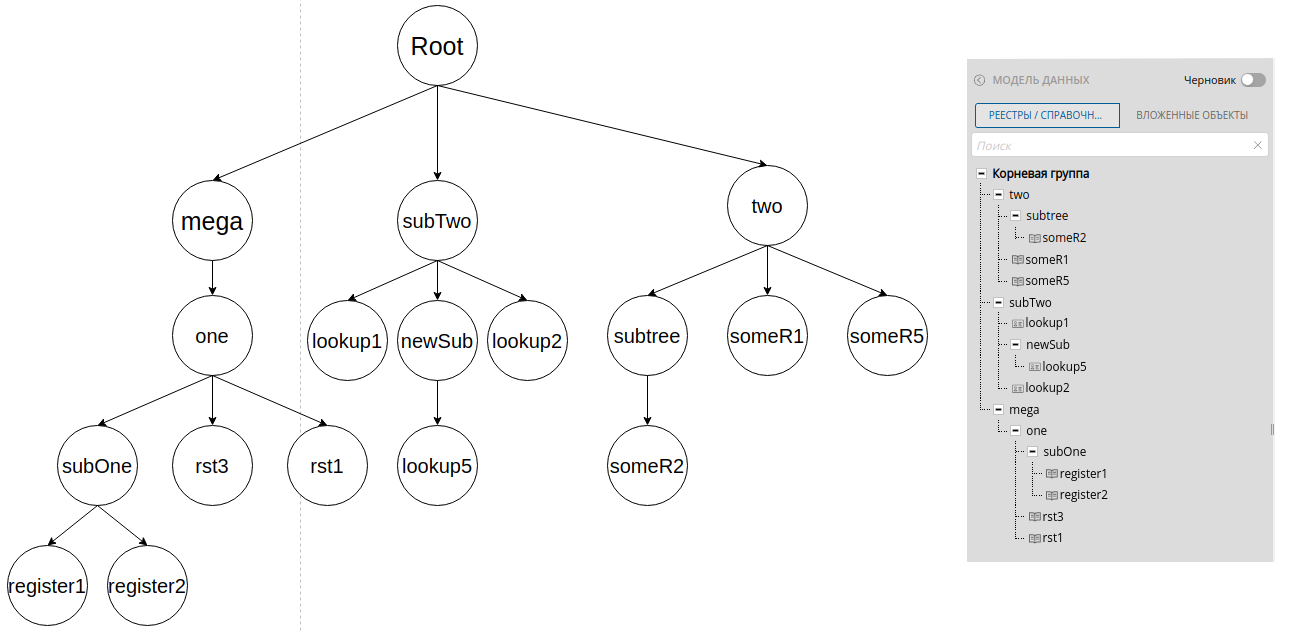
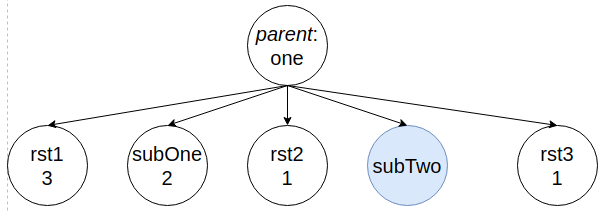
При помощи diffService определяются измененные узлы дерева entity groups. При этом они оборачиваются в обертки, которые хранят расстояние до других узлов того же уровня и имя родительского узла. Отдельно хранятся расстояния до измененного и после измененного узла:

{
parent: "one",
siblingBefore: {
   rst1: 3,
   subOne: 2,
   rst2: 1
},
siblingAfter: {
   rst3: 1
}
}

Благодаря этой обертке, при слиянии дерева, узел subTwo найдет место внутри родителя one, рядом с ближайшим из его потомков.

После создания такой обертки для каждого измененного узла, формируются поддеревья. В кейсе будет сформировано одно поддерево, но если изменения будут в разных концах, то будет сформировано несколько поддеревьев и они по очереди будут вливаться в основное дерево.

Сформированное поддерево из оберток изменений:

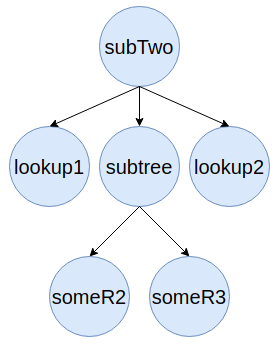
Алгоритм начинает вливание в основное дерево, начиная с корня поддерева subTwo. Производится поиск родителя subTwo - one:

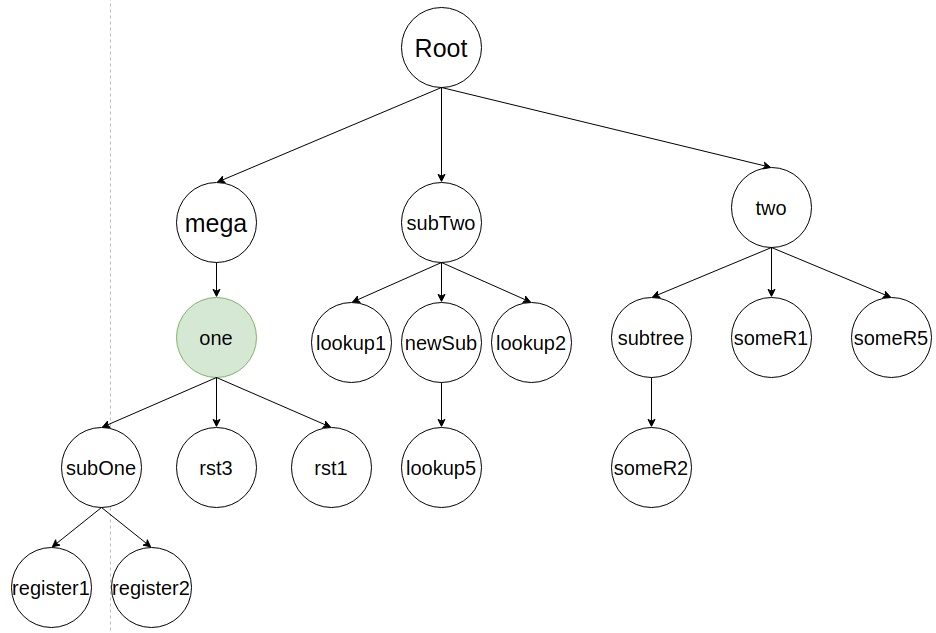
Если бы узла не было, то поддерево бы вливалось в корень Root. Далее алгоритм вливает узел subTwo.

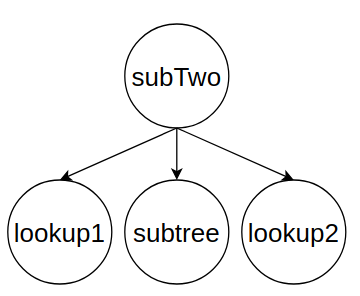
Алгоритм ищет в дереве его старую версию и удаляет ее.

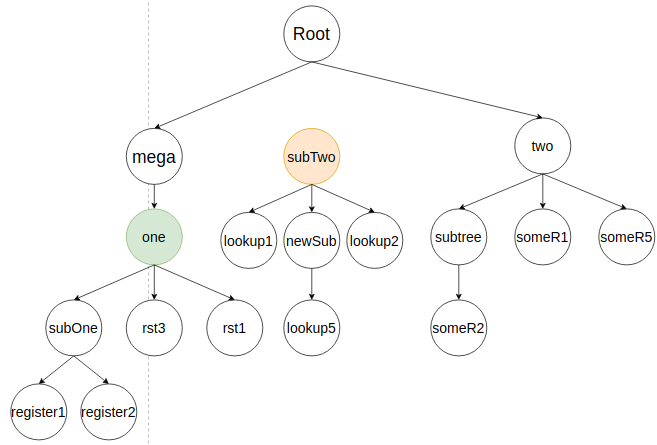
Затем вставляет узел subTwo внутрь своего родителя one и обходит всех потомков и анализируя какой из них ближе.

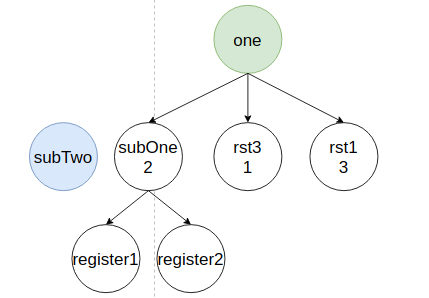
Место расположения не является лучшим, потому что слева и справа нет соседей, которые указаны в обертке. Справа стоит subOne, но он должен быть левее вставляемого элемента на два узла, а в рассматриваемом случае он правее. Единственная ситуация, которая будет считаться лучше рассматриваемой, если слева будет стоять элемент, расстояние до которого один узел. Сейчас в алгоритме при равных расстояниях до соседних узлов, предпочтение отдается узлу с левой стороны.

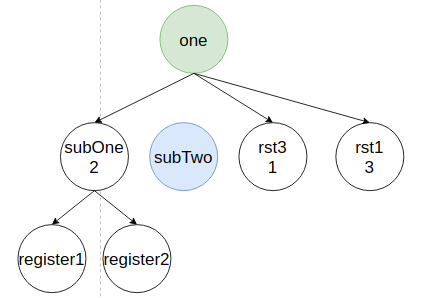
После вставки узла subTwo ему присваиваются наследуемые узлы.

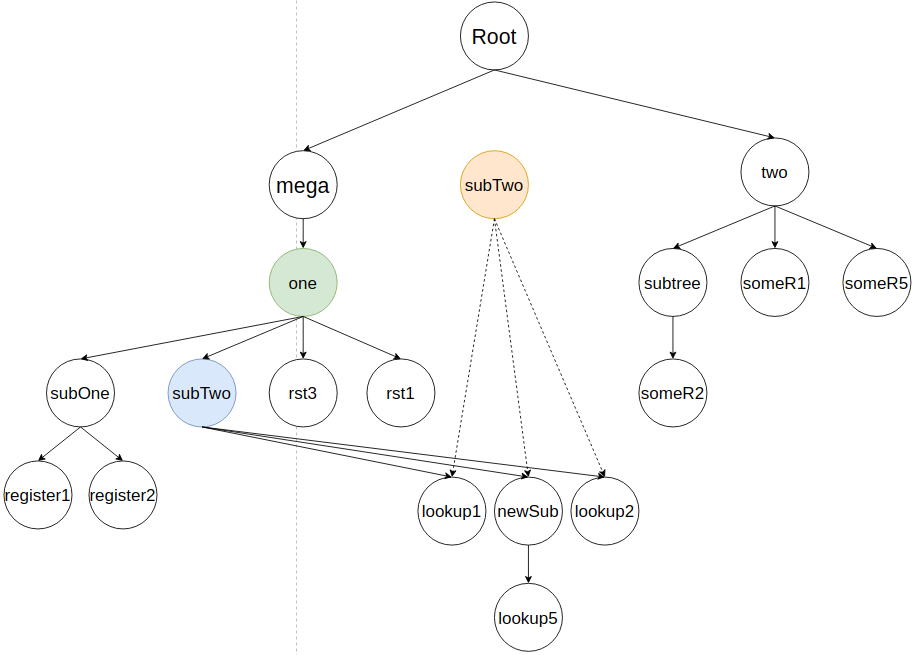
Затем вливается следующий элемент поддерева lookup1, как потомок subTwo. Алгоритм ищет прошлое представление узла в дереве и удаляет его.

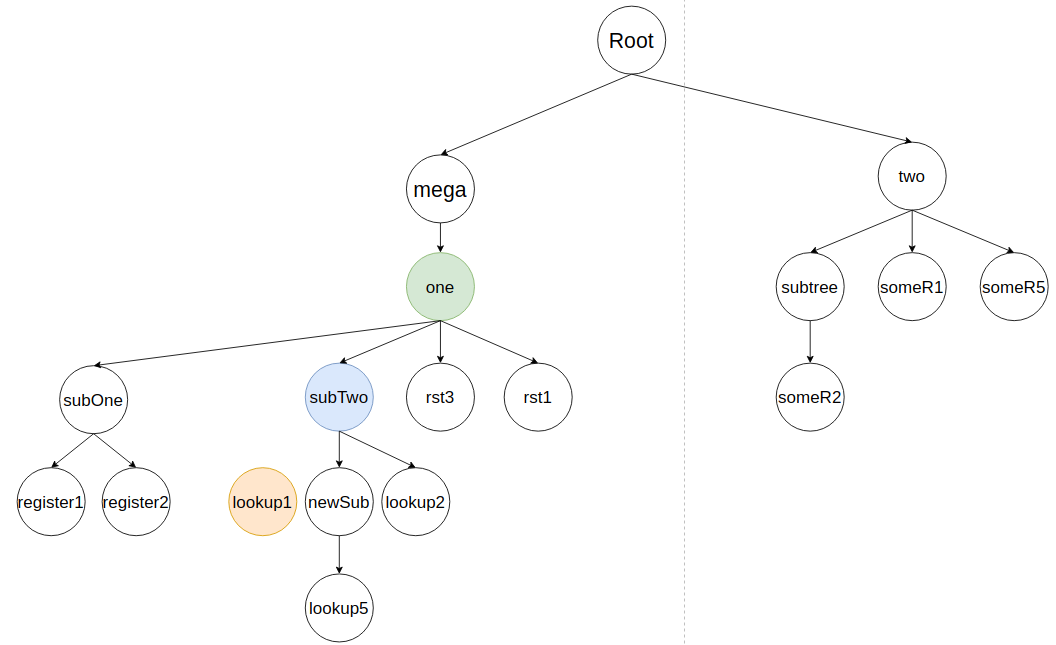
Узел lookup1 вставляется в соответствии с близостью к своим соседям. В кейсе самым близким будет lookup2 справа на два элемента. По этому lookup1 будет влит следующим образом:

Если у lookup1 были бы еще узлы, то алгоритм занимался бы их вливанием. В рассматриваемом кейсе их нет, поэтому он возвращается к потомкам subTwo. Следующий в очереди потомок subTree. Алгоритм ищет в дереве предыдущий subTree и удаляет его.

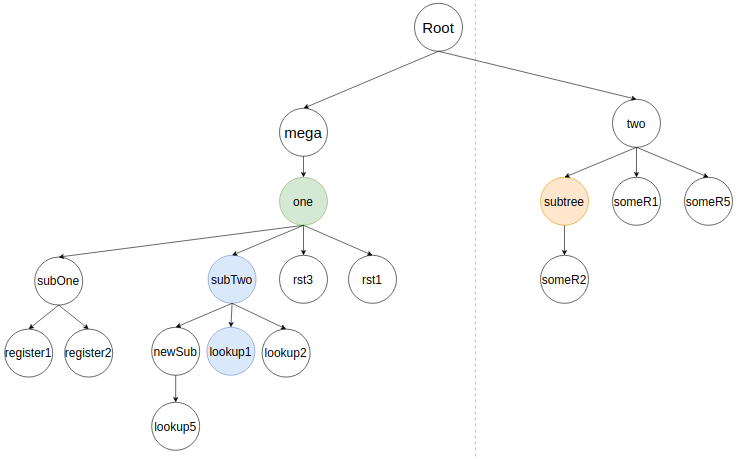
Алгоритм вставляет subTree, как потомка subTwo в соответствии с его соседями. Идеальная позиция, когда lookup1 расположен слева. Результат вставки:

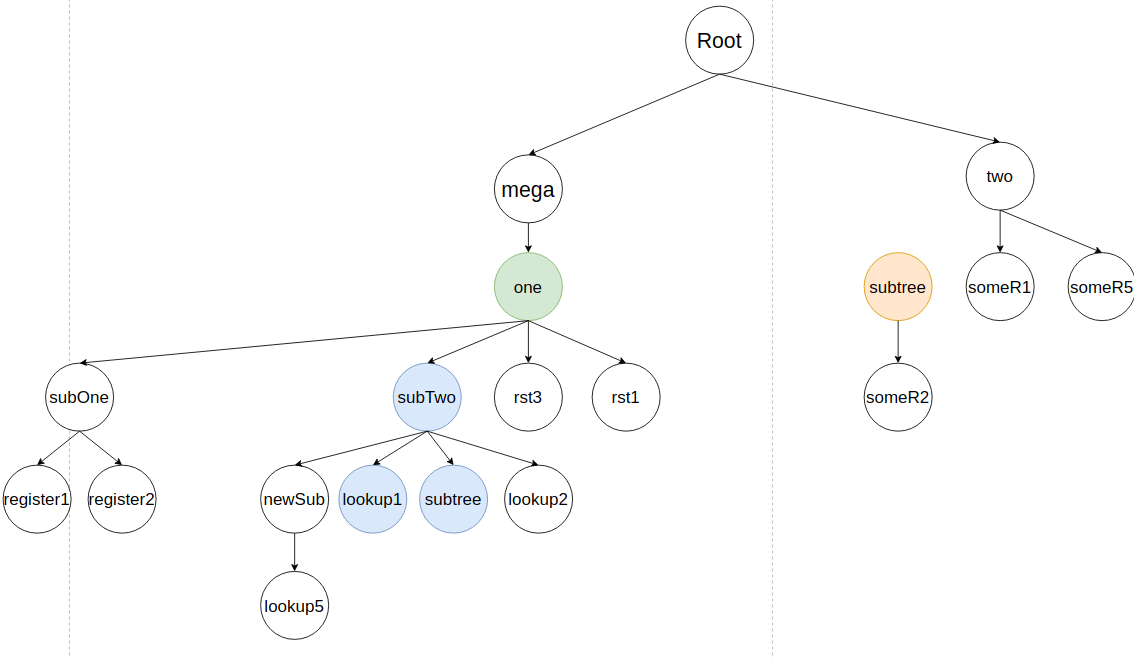
Алгоритм присваивает узлы удаленного subTree:

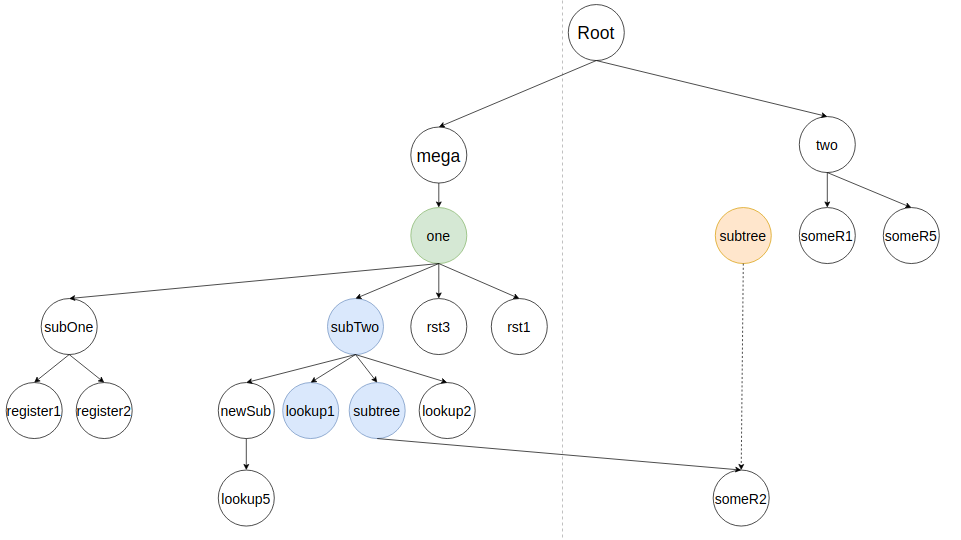
Алгоритм начинает вливание узла subTree и начинает с someR2, где ищет его предыдущее представление для удаления.

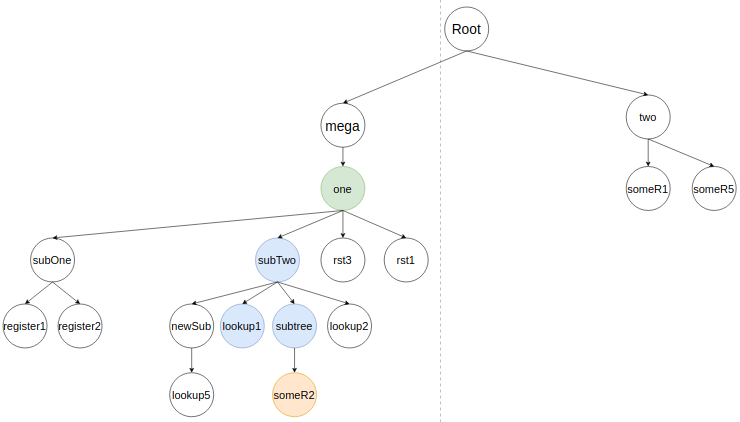
Затем алгоритм вставляет someR2, как узел subTree. В этом кейсе не будет найдено ближайших элементов (потому что у subTree отсутствуют потомки), значит someR2 будет вставлен как последний (самый правый) потомок.

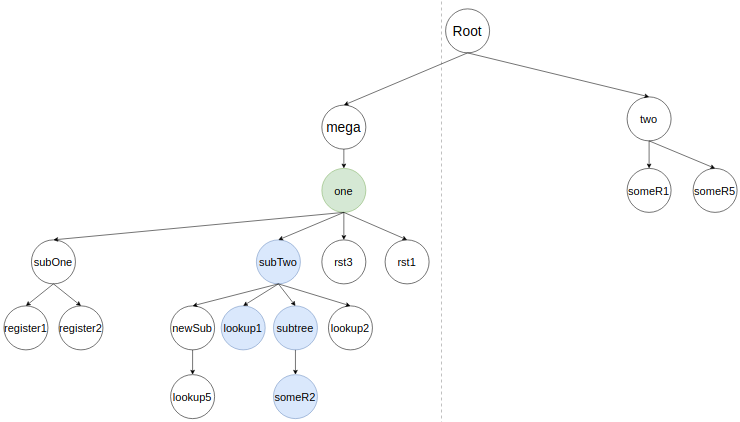
У someR2 нет потомков - алгоритм продолжает работу с потомками subTree и занимается вливанием someR3. Он не найдет в дереве его предыдущего представления, потому что someR3 был добавлен в черновике пользователя, поэтому никакой узел из дерева не удаляется. Узел someR3 будет вставлен, как потомок subTree. Лучшая позиция, в которой слева стоит someR2. Результат вставки:

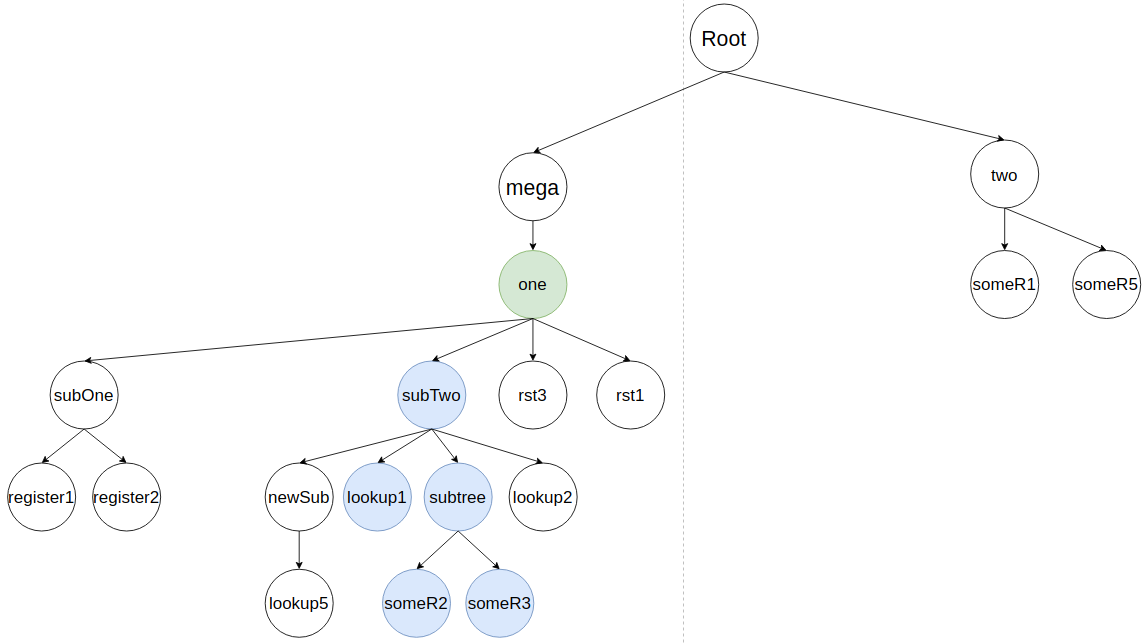
У subTree закончились его потомки и алгоритм возвращается к вливанию потомков subTwo, где узел lookup2 будет влит аналогично lookup1.

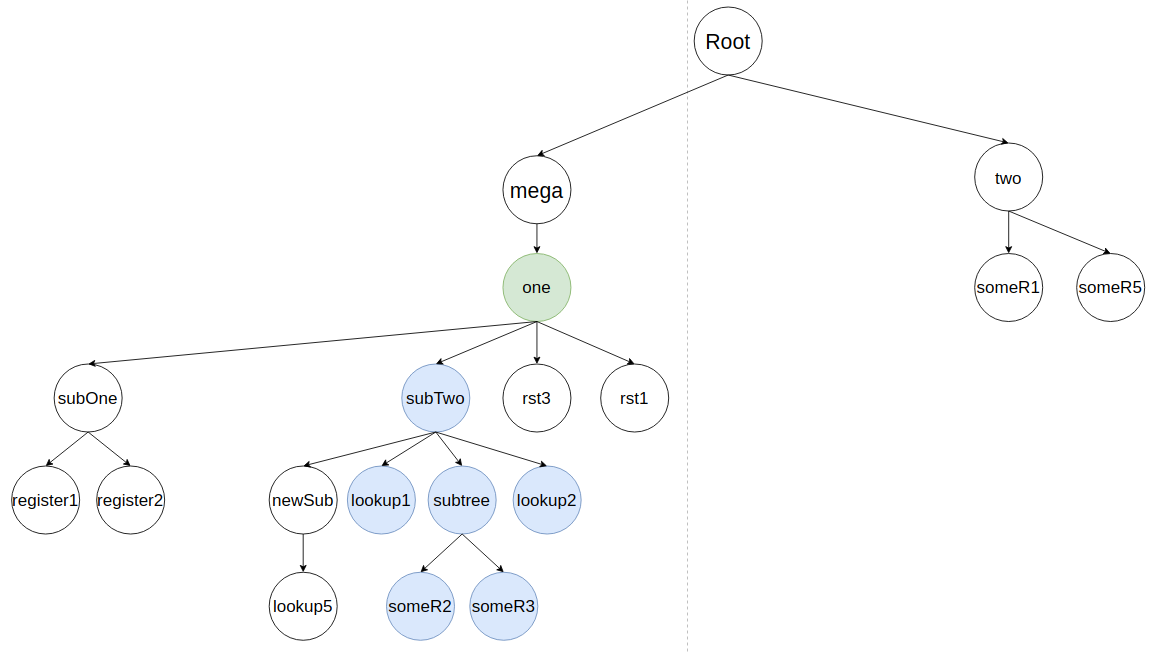
Итоговый результат: